
En computación, las operaciones lógicas son necesarias porque se pueden usar para modelar la forma en que la información fluye a través de los circuitos eléctricos, como los circuitos dentro de una CPU. Estos tipos de operaciones se denominan operaciones booleanas.
Los elementos de un circuito que se comportan de acuerdo con la lógica booleana se denominan puertas lógicas.
Operaciones lógicas fundamentales.
Las siguientes siete operaciones lógicas toman entradas que son verdaderas (1) o falsas (0) y producen un único valor de salida que también es verdadero o falso.
La mayoría de estas operaciones pueden tomar más de dos entradas, excepto la operación NO que solo toma una entrada. A continuación se muestran ejemplos que usan solo una o dos entradas, que es lo que generalmente ocurre dentro de una computadora.
Las operaciones se enumeran a continuación. Haga clic en un enlace para una operación para obtener más información.
- Y
- O
- NO
- NAND
- NI
- XOR
- XNOR
La operación lógica AND devuelve verdadero solo si todas sus entradas son verdaderas. Si alguna de las entradas es falsa, la salida también es falsa.
En la programación de computadoras, la operación AND generalmente se escribe como && (dos ampersands).
En el álgebra booleana, la operación AND de dos entradas A y B se puede escribir como AB .
A continuación se muestra la tabla de verdad para una operación AND de dos entradas y el diagrama del circuito de una compuerta lógica AND.

| Y | ||
|---|---|---|
UNA | segundo | AB |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
O
La operación lógica OR devuelve verdadero si alguna de sus entradas es verdadera. Si todas las entradas son falsas, la salida también es falsa.
En programación de computadoras, la operación OR generalmente se escribe como || (dos barras verticales).
En el álgebra booleana, el valor OR de dos entradas A y B se puede escribir como A + B.
Nota: No confunda la operación OR con la suma aritmética, aunque ambas usen el símbolo " + ". Son operaciones distintas.
A continuación se muestra la tabla de verdad para una operación OR de dos entradas y el diagrama del circuito de una puerta lógica OR.

| O | ||
|---|---|---|
UNA | segundo | A + B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
NO
La operación lógica NOT devuelve verdadero si su entrada es falsa, y falso si su entrada es verdadera.
En la programación de computadoras, la operación NO se escribe como ! (un signo de exclamación).
En el álgebra booleana, el valor NO de una entrada A puede escribirse como A̅ (A con un sobrepaso).
A continuación se muestra la tabla de verdad para una operación NO, y el diagrama del circuito de una puerta lógica NO.

NAND
La operación lógica NAND (que significa "NO Y") devuelve verdadero si alguna de sus entradas es falsa, y falso si todas sus entradas son verdaderas.
En el álgebra booleana, el valor NAND de dos entradas A y B se puede escribir como

NAND tiene la distinción de ser una de las dos puertas lógicas "universales" porque cualquier otra operación lógica se puede crear utilizando solo puertas NAND. (La otra puerta lógica universal es NOR.)
A continuación se muestra la tabla de verdad para una operación NAND de dos entradas y el diagrama del circuito de una puerta lógica NAND.

| NAND | ||
|---|---|---|
UNA | segundo | ___ AB |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NI
La operación lógica NOR (que significa "NO O") devuelve verdadero si todas sus entradas son falsas, y falso si alguna de sus entradas son verdaderas.
En el álgebra booleana, el valor NOR de dos entradas A y B se puede escribir como
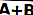
NOR tiene la distinción de ser una de las dos puertas lógicas "universales", ya que cualquier otra operación lógica se puede crear utilizando solo puertas NOR. (La otra puerta lógica universal es NAND.)
A continuación se muestra la tabla de verdad para una operación NOR de dos entradas y el diagrama del circuito de una puerta lógica NOR.

| NI | ||
|---|---|---|
UNA | segundo | _____ A + B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
La operación lógica XOR (que significa "OR exclusivo") devuelve verdadero si alguna de sus entradas es diferente, y falso si son todas iguales. En otras palabras, si sus entradas son una combinación de verdadero y falso, la salida de XOR es Si sus entradas son todas verdaderas o todas falsas, la salida de XOR es falsa.
En el álgebra booleana, el valor XOR de dos entradas A y B se puede escribir como A⊕B . (El símbolo XOR, ⊕, se asemeja a un signo más dentro de un círculo.)
A continuación se muestra la tabla de verdad para una operación XOR de dos entradas y su diagrama de circuito:

| XOR | ||
|---|---|---|
UNA | segundo | A⊕B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
La operación lógica XNOR (que significa "Exclusive NOT OR" devuelve true si todas sus entradas son iguales, y false si alguna de ellas es diferente. En otras palabras, si sus entradas son una combinación de true y false, la salida de XNOR es falso. Si sus entradas son todas verdaderas o todas falsas, la salida de XNOR es verdadera.
En el álgebra booleana, el valor XNOR de dos entradas A y B se puede escribir como

A continuación se muestra la tabla de verdad para una operación XNOR de dos entradas y su diagrama de circuito:

| XNOR | ||
|---|---|---|
UNA | segundo | _____ A⊕B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
- ¿Cómo creo un programa de computadora?
Acumulador, booleano, idempotencia, operador, términos de programación
